Esta nota técnica tiene como propósito poner de manifiesto la importancia de considerar el proceso de transferencia de calor completo, además de las propiedades térmicas, cuando se lleva a cabo la selección de aislantes con fines de ahorro de energía.
Dr. Juan Antonio Aguilar Garib
Se toman en cuenta aspectos adicionales a la popular “R” y también la práctica de operación del sitio en donde esté el aislante, si va a trabajar de modo intermitente o continuo, pues esto también es importante en la contabilidad de calor que un equipo dado debe extraer de un sitio acondicionado. Las ecuaciones que se presentan tienen la intención de simplificar el análisis que se ofrece aquí, tienen además un propósito ilustrativo, como las figuras, no es la intención resolverlas y solamente hay que observar los términos que se explican en esta nota.
La conductividad térmica (k) define la capacidad que tiene un material para transferir calor según la ecuación de Fourier.
q es la tasa de transferencia de calor, A es el área de transferencia, DT es la diferencia de temperatura entre las caras (T1 y T2) y Dx es el espesor. En este caso se supone que la transferencia de calor se da en una sola dirección. Así los aislantes son aquellos materiales que tienen K pequeña.
Al igual que en un sistema eléctrico la resistencia se incrementa con la longitud, en la transferencia de calor la resistencia térmica aumenta con el espesor con lo que la ecuación (1) se podría reescribir como:
El mercado se rige en este aspecto por este valor R, que es directo y da una oportunidad de obtener altos valores de R simplemente aumentando el espesor y así tener un aislante en apariencia mejor. Dado que existen muchísimas combinaciones entre el espesor y la conductividad térmica que proporcionan una R dada, es necesario saber qué es lo más conveniente, conductividades altas compensadas con espesores grandes, o tal vez sea mejor tener espesores pequeños con conductividades pequeñas. Para poder contestar esta pregunta se debe considerar que la diferencia de temperatura es la fuerza motriz para el transporte de calor (ecuaciones 1 y 2), pero que además existe un término de extracción de calor que se refiere al que está almacenado en el material y que depende de la temperatura a la que se encuentra éste al inicio del proceso de transferencia. Esta parte está gobernada por la difusividad térmica y proporciona el tiempo que será necesario para llegar al momento en que el perfil de temperatura en la pared no cambia con el tiempo, y que es la única condición en que la R gobierna la transferencia de calor. La extracción de calor que un equipo hace del lado frío de esta pared, por ejemplo, está dada por el total de estas dos contribuciones, y es la que se busca minimizar para propósitos de ahorro de energía.
La solución que proporciona la temperatura en cualquier punto del material considerando desde el inicio del calentamiento, o enfriamiento, es:
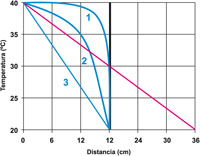
En esta ecuación T1 y T2 son las temperaturas en las caras del material, x es la posición dentro del material (entre las caras), L es el espesor, Dh, es una constante que depende de las condiciones de inicio, lh es una constante geométrica que para este caso depende del espesor del material, k es, por fin, la difusividad térmica, y t es el tiempo que ha transcurrido desde que se inicia el proceso de transferencia de calor. En esta ecuación lo único que se debe tener presente es que los primeros dos términos corresponden al perfil conocido como de “estado estable” el cual indica que ha transcurrido suficiente tiempo, en rigor infinito, para que la temperatura ya no cambie con el tiempo. El estado que se tiene durante este tiempo se conoce como “estado transitorio”. La figura 1 muestra el perfil lineal del estado estable para dos espesores de material con la misma diferencia de temperatura, sin importar de qué material se trate la temperatura sigue este perfil. Como la diferencia de temperatura es la misma en los dos casos, la transferencia es el doble para el que tiene 18 cm de espesor en comparación al de 36 cm, de manera que aquí todo depende de R.
|
|
| Figura 1. Perfil de temperatura para el caso de dos espesores, señalados aquí como distancia, de material. La línea 1 es para 18 cm y la línea 2 es para 36 cm (escogidos para fines ilustrativos) con la misma diferencia de temperatura entre caras (20° C). |
La exponencial en el último término de la ecuación 4, la que contiene al tiempo, se hace más pequeña y tiende a cero conforme el tiempo avanza. También hay muchas combinaciones posibles de lhkt (aquí se omitió la h en lh para simplificar, pero es la misma) que hacen que la exponencial se anule, sabiendo que ln es constante (vale hp/L) entonces la competencia queda entre la difusividad (k) y el tiempo (t). La difusividad sí depende del material según:
En esta ecuación r es la densidad y C es el calor específico del material. Una vez más hay muchísimas combinaciones de conductividad, densidad y calor específico que pueden resultar en la misma difusividad. ¿Y cuál es la mejor?. Si se tiene un material de conductividad alta se tendrá una difusividad alta y el término l2kt hará que a tiempo corto se haya llegado al estado estable. Ya que la energía que se está extrayendo durante este tiempo proviene del material en sí, éste aún no está trabajando como aislante, así que sería deseable que se llegue rápidamente al estado estable, por otra parte conductividades altas implican mayor transferencia de calor durante ese estado. ¿Qué hay con seleccionar materiales de baja densidad (r) o de calor específico (C) menor?. Estos términos corresponden al calor almacenado, así que si se selecciona un material aislante lo mejor será que la difusividad sea alta debido a la baja densidad y calor específico del material. Como ya se mencionó l depende del espesor y entonces el término l2kt, aumenta conforme el espesor (L) disminuye, lo que sugiere que es mejor tener aislantes delgados, pero eso haría que la tasa de transferencia aumentara en el estado estable.
|
|
| Figura 2. Perfiles de temperatura considerando el estado transitorio, la curva 1 corresponde a un términol2ktmenor que la curva 2. La línea recta (3) corresponde al estado estable. |
La figura 2 muestra los perfiles que se tienen durante el estado transitorio para el caso del material de 18 cm de espesor, se supone que la condición inicial es que el material se encuentra a una temperatura uniforme de 40° C. En esa figura la línea recta corresponde al estado estable, en rigor se requiere que el término l2kt sea infinito, pero en la práctica basta con que sea del orden de 10 para que el perfil sea el del estado estable. Si el material es el mismo se puede decir que la curva 1 es para un tiempo menor que la curva 2, o bien si se trata de materiales diferentes del mismo espesor se puede decir que la curva 1 es para el que tiene la menor K, mayor R, que la curva 2.
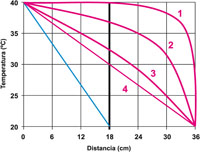
La figura 3 muestra lo mismo que la figura 2, pero con mayor espesor (36 cm) lo que significa una R mayor, pero dado que el espesor es mayor para las mismas condiciones se tendrá un transitorio mayor, es decir que estaremos extrayendo más tiempo, más calor, del material que del ambiente.
|
|
| Figura 3. Perfiles de temperatura considerando el estado transitorio, la curva 1 corresponde a un términol2kt menor que las curvas 2 y 3. La línea recta (4) corresponde al estado estable. |
Las ecuaciones y gráficas que se presentaron permiten tener una idea de la validación de R, que es muy importante pero debe ser considerada con otras cosas, si por ejemplo el cálculo trata de la pared de un horno industrial que va a operar durante varios años consecutivos, no es necesario preocuparse por el estado transitorio ya que el horno operará en estado estable, aquí se puede utilizar a la R simultáneamente como criterio de aislamiento y de ahorro de energía. Pero en los lugares en que los equipos de refrigeración o de aire acondicionado se encienden intermitentemente, como es el caso del uso doméstico, se deben tomar en cuenta otras propiedades del aislante además de la R. Aquí se aprecia por qué es común que los aislantes sean de baja densidad y de bajo calor específico, la idea es que no haya mucho calor almacenado y se debe resistir la tentación de aumentar el espesor del aislante sin mayor análisis. En general, si el aislante es delgado requiere tener una conductividad térmica muy baja. En este escrito no se consideran, pero también es importante dentro de la operación, a la radiación, las paredes compuestas y los coeficientes de película o de interface. La mejor combinación de propiedades también involucra a la rutina con la que se acondicionan térmicamente los espacios. Aunque lo ideal sería poder seleccionar combinaciones óptimas para todos los parámetros, la realidad es que tenemos la restricción que el mercado impone y solamente podemos seleccionar entre los materiales que éste ofrece, aún así es posible proponer, en base a un análisis del tipo del que se ha presentado aquí, lo más adecuado. Cada vez que se arranca un aire acondicionado se debe extraer el calor que el material de los muros ha almacenado, o depositarlo si se trata de una calefacción. Como comentario final hago mención de que esto es inevitable, pero dado que la transferencia de calor, ya sea ganancia si estamos enfriando o pérdida si estamos calentando, depende de la diferencia de temperatura, es suficiente con disminuir esta diferencia para ahorrar energía, el sobre enfriamiento o sobrecalentamiento, muchas veces innecesario, va más allá de lo que ningún material aislante puede resolver.
——————————————————————————-